作 者:老余捞鱼
原创不易,转载请标明出处及原作者。

写在前面的话:今天给大家带来一篇更深入、更好玩的现代组合理论(MPT)实战攻略,用最接地气的示例和代码,教你玩转现代组合理论:从数据获取、Sharpe筛选、Riskfolio优化,到效率前沿可视化,最终开发出年化35%+、波动<20%的最优组合“智配通”Pro。
一、MPT:投资界的科学魔法
我发现70年前一个数学公式,至今让基金经理们偷偷赚钱。
1952年,马科维茨在菜场获得灵感。当大妈说”鸡蛋别放一个篮子”,他追问:”怎么放最稳妥?” 于是诞生了现代投资组合理论(MPT)——后来拿了诺贝尔奖。

当时,投资者大多靠直觉或小道消息选股,而马克维茨用数学方法证明:通过合理搭配资产,可以在不增加风险的情况下提高回报。这一发现不仅让他在1990年拿下诺贝尔经济学奖,也彻底改变了投资的游戏规则。
很多人以为买一堆股票就是分散,其实大错特错!
MPT不只是“分散投资”,而是“最佳分散投资”。最关键的不是把鸡蛋放满篮子,而是找到负相关(Correlation)资产。
举个例子:
☀ 晴天:🍦冰淇淋公司 ↗️,☂️雨伞公司 ↘️
🌧 雨天:🍦冰淇淋公司 ↘️,☂️雨伞公司 ↗️晴天冰淇淋卖得好,雨伞卖得差;雨天则相反。这种“负相关”就是分散投资的精髓。
这就是真正的多样化。同理,很多人误以为买10只科技股就是分散投资,其实它们可能一起涨跌,根本没降低风险!
| 组别 | 配置资产 | 典型风险 | 典型收益 |
|---|---|---|---|
| 随机分散 | 同一行业多只股票 | 行业整体下跌风险高 | 与市场同步 |
| 最优多样化 | 行业A + 行业B + 大宗商品 | 不同行业/资产间负相关降风 | 更平滑的收益曲线 |
MPT虽然经典,但这40多年来也在不断进化:
- 套利定价理论(APT):认为收益由多个因素驱动,如市场趋势,推动了智能beta策略。
- 经济周期:根据经济周期调整投资组合,比如用OECD指标预测市场趋势。
- ARCH模型:关注波动性变化,提醒我们在危机时分散效果可能减弱。
- 优化陷阱:优化结果依赖输入数据,需谨慎选择以避免错过次优组合。
- 长期 vs 短期:长期投资者的风险-回报权衡不同,需考虑投资期限。
这些进展让MPT更适应现代市场,但核心理念不变:科学分散,理性投资。
二、手把手教学:让MPT活起来
现在,我们用代码把MPT变成现实!以下是实现步骤,下面的代码基于澳大利亚股市数据,稍作调整也能用在A股或港股。
步骤1:收集和准备数据
我们需要历史股价数据来分析。以下代码获取过去5年的股票收盘价:
# 定义日期范围(从今天起 5 年前)
from datetime import datetime, timedelta
import yfinance as yf
end_date = datetime.now().strftime('%Y-%m-%d')
start_date = (datetime.now() - timedelta(days=5*365)).strftime('%Y-%m-%d')
# 下载数据
data = yf.download(all_assets, start=start_date, end=end_date, auto_adjust=False)
data = data.loc[:, ('Adj Close', slice(None))]为什么选5年?太短数据不可靠,太长可能过时,5年是“刚刚好”的时间段。
步骤2:计算每日收益率
接下来,把股价变化转为收益率,并年度化:
# 计算每日收益
returns = data.pct_change().dropna()
# 年化收益和标准差
trading_days_per_year = 252
annualized_returns = returns.mean() * trading_days_per_year
annualized_volatility = returns.std() * np.sqrt(trading_days_per_year)这里把每日收益率乘以252(一年交易日数),波动率用平方根缩放,这是金融学的基本原理。
步骤3:计算夏普比率
神奇公式:性价比 = (收益 – 保本收益)/ 波动风险
专业词叫”夏普比率”,我管它叫“投资性价比”,夏普比率衡量每单位风险带来的额外回报:
risk_free_rate = 0.04 # 假设无风险利率4%
sharpe_ratios = (annualized_returns - risk_free_rate) / annualized_volatility
# 按夏普比率选择前 12 只股票
top_n = 12
top_stocks = sharpe_ratios.sort_values(ascending=False).head(top_n).index.tolist()以下是澳大利亚股市前12只股票的夏普比率(示例数据):
| 股票代码 | 公司名称 | 夏普比率 |
|---|---|---|
| TLX.AX | Telix Pharmaceuticals | 1.17 |
| CBA.AX | Commonwealth Bank | 1.02 |
| CPU.AX | Computershare | 0.93 |
| NAB.AX | National Australia Bank | 0.87 |
| WTC.AX | WiseTech Global | 0.85 |
| PLS.AX | Pilbara Minerals | 0.82 |
| BXB.AX | Brambles | 0.77 |
| QBE.AX | QBE Insurance | 0.76 |
| ALL.AX | Aristocrat Leisure | 0.74 |
| WBC.AX | Westpac Banking | 0.72 |
| WES.AX | Wesfarmers | 0.69 |
| ANZ.AX | ANZ Banking Group | 0.67 |
普比率告诉我们,我们承担每单位风险能获得多少额外回报。生物科技公司Telix以1.17领先,但银行股也表现不俗。
步骤4:构建投资组合
我们用riskfolio库创建投资组合对象,计算预期收益率和协方差矩阵:
# 构建投资组合对象
import riskfolio as rp
port = rp.Portfolio(returns=returns)
# 选择方法并估计输入参数
method_mu = 'hist' # 根据历史数据估计预期收益的方法
method_cov = 'hist' # 根据历史数据估计协方差矩阵的方法
port.assets_stats(method_mu=method_mu, method_cov=method_cov)这就像给投资组合装上“发动机”,准备优化!
步骤5:优化投资组合
现在,找到最大化夏普比率的投资组合:
w = port.optimization(model='Classic', rm='MV', obj='Sharpe', rf=0, hist=True)这就是诺贝尔奖的魔力!我们告诉算法:“找到最大化夏普比率的投资组合权重。” 优化结果如下:
| 股票代码 | 公司名称 | 权重 (%) |
|---|---|---|
| CBA.AX | Commonwealth Bank | 29.40 |
| CPU.AX | Computershare | 17.62 |
| BXB.AX | Brambles | 16.71 |
| TLX.AX | Telix Pharmaceuticals | 16.57 |
| PLS.AX | Pilbara Minerals | 7.88 |
| WTC.AX | WiseTech Global | 7.17 |
| QBE.AX | QBE Insurance | 4.65 |
| NAB.AX | National Australia Bank | 0.00 |
| ALL.AX | Aristocrat Leisure | 0.00 |
| WBC.AX | Westpac Banking | 0.00 |
| WES.AX | Wesfarmers | 0.00 |
| ANZ.AX | ANZ Banking Group | 0.00 |
惊讶吗?只有6只股票有权重!这是因为优化器发现其他股票在风险-回报组合上“多余”,用数学筛选掉了“冗余”资产,留下最能互补的。
步骤6:可视化效率前沿
可视化“效率前沿”是MPT的精髓,展示风险和回报的最佳组合:
import matplotlib.pyplot as plt
# 构建效率前沿
ef = port.efficient_frontier(model='Classic', rm='MV', points=50, rf=rf, hist=True)
plt.plot(ef['Volatility'], ef['Return'])
plt.scatter(w.volatility, w.returns)
plt.title('效率前沿与最优点')
plt.xlabel('年化波动')
plt.ylabel('年化收益')
plt.show()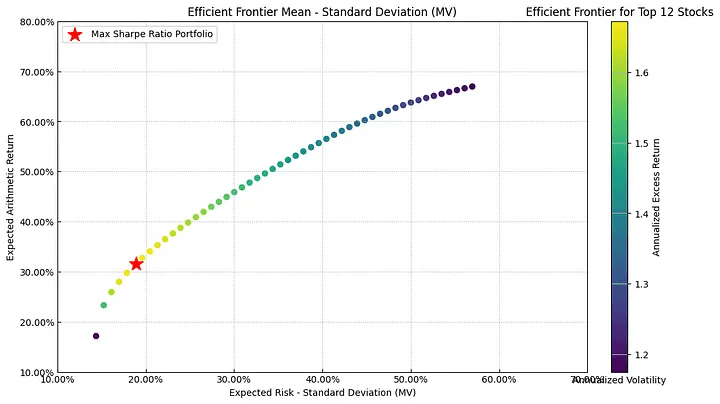
上图生成了一条曲线,标出最佳投资组合(红星)。
三、实战结果&实用建议
下面是实战后的数据结果:
🔍 优化投资组合表现:
📈 预期年化收益率:35.49%
⚠️ 年化波动率:18.87%
🎯 夏普比率:1.67
🚀 超额收益(对比 4.00% 无风险收益率):31.49%
性价比(夏普比率)1.67意味着什么?
<1.0:风险回报不佳;1.0-2.0:优秀表现;2.0:极罕见。
MPT的实用建议
1. 要做的事:
- 用好数据:5年历史数据是最佳选择,太短不可靠,太长可能过时。
- 定期调整:市场变化快,定期重新计算组合权重。
- 考虑交易成本:理论无成本,现实中要算上手续费。
2.不要做的事:
- 别假设相关性不变:2008年危机时,资产相关性突然飙升,分散失效。
- 别忽视黑天鹅:MPT假设正态分布,但市场可能出现极端事件。
- 别忘了流动性:理论上完美的组合,若无法买卖就没用。
3.下一步行动
准备好用MPT升级你的投资了吗?可以从下面这三点开始:
- 检查你的投资组合:是否真正分散?
- 计算夏普比率:你的风险回报合理吗?
- 分析相关性:你的资产是“同进退”还是“互补”?
四、观点总结
现代组合理论(MPT)是投资界的经典工具,通过数学方法帮你平衡风险和回报。它的核心是分散投资,关注资产相关性,找到最佳组合。尽管它假设市场回报呈正态分布,可能忽视极端事件,但通过定期调整和结合最新进展(如PMPT),它依然是投资者的得力助手。
- 科学投资:用数学取代直觉,优化风险-回报。
- 分散为王:选择低相关资产,降低整体风险。
- 动态调整:市场变化,组合需定期优化。
- 注意局限:警惕黑天鹅事件和交易成本。
- 实践第一:用代码试试,亲手打造你的财富蓝图!
本文提供了完整详实的源代码中文注释和功能结构及使用说明,确保您能读懂代码的含义并能根据自身需求进行改写。
还等什么,立即行动起来!需要完整源代码请后台留言!
#关键词:#理财干货 #MPT #资产配置 #投资组合 #小白理财 #量化投资 #财富思维 #避坑指南 #投资策略 #分散投资 #夏普比率 #有效前沿 #财富管理 #澳洲股市 #澳大利亚股票
读到最后,希望这篇文章为您带来了新的启发和实用的知识!如果觉得有帮助,请不吝点赞和分享,您的支持是我持续创作的动力。祝您投资顺利,收益长虹!如果对文中内容有任何疑问,欢迎留言,我会尽快回复!
本文内容仅限技术探讨和学习,不构成任何投资建议。
Be First to Comment