我拆解了15只美股科技巨头，用量化方法发现投资AI股的真相（中）

作 者：老余捞鱼

原创不易，转载请标明出处及原作者。

写在前面的话：最近AI概念火到不行，但你是不是也在疑惑：这些科技公司到底值不值得投资，还只是市场炒作？今天我就用Python量化方法来拆解美国前15大科技股，从财务分析到市场估值，从业绩表现到风险水平和公众热度，只需六步拆解它们的价值，帮你避泡沫、投真金，投前必看。

在上一篇文章中我们对这15家公司完成了两项分析：

• 1. 财务健康度：看看这些公司赚钱能力怎么样。
• 2. 市场估值：分析股价是否虚高；

本篇中我们将继续进行这三项内容的分析：

• 3. 风险水平：衡量投资这些公司的风险。
• 4. 业绩表现：回顾历史收益情况。
• 5. 最大回撤：你能承受多大亏损？

第三步：风险水平，谁能笑到最后？

投资不仅要看收益，还要看风险。我用了6种不同的方法来计算这些股票的波动率：

1. 标准差；
2. 帕金森波动率；
3. Garman-Klass波动率；
4. Hodges-Tompkins波动率；
5. Rogers-Satchell波动率；
6. Yang-Zhang波动率。

3.1 标准差的作用是衡量收益与平均收益的差距有多大。

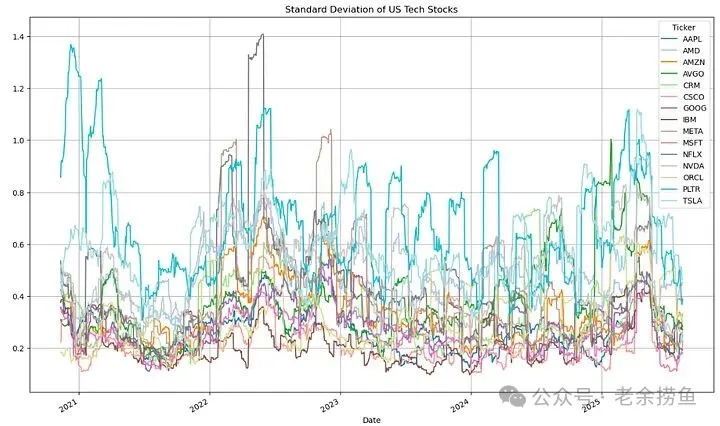
实现代码如下：

#Reading data
ticker_list = ['NVDA','MSFT','AAPL','GOOG','AMZN','META','AVGO','TSLA','ORCL','NFLX','PLTR','AMD','CSCO','CRM','IBM']

data = yf.download(
    ticker_list, 
    start="2020-01-01", 
)
adj_close = data['Close']

#Standard deviation

import math
def standard_deviation(price_data, window=30, trading_periods=252, clean=True):
    log_return = (price_data/ price_data.shift(1)).apply(np.log)
    result = log_return.rolling(window=window, center=False).std() * math.sqrt(
        trading_periods
    )
    if clean:
        return result.dropna()
    else:
        return result
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
standard_deviation(adj_close).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Standard Deviation of US Tech Stocks')
plt.show()

3.2 帕金森波动率是在使用最高价和最低价，而不是仅仅使用特定时期内的收盘价来估计回报的波动性。

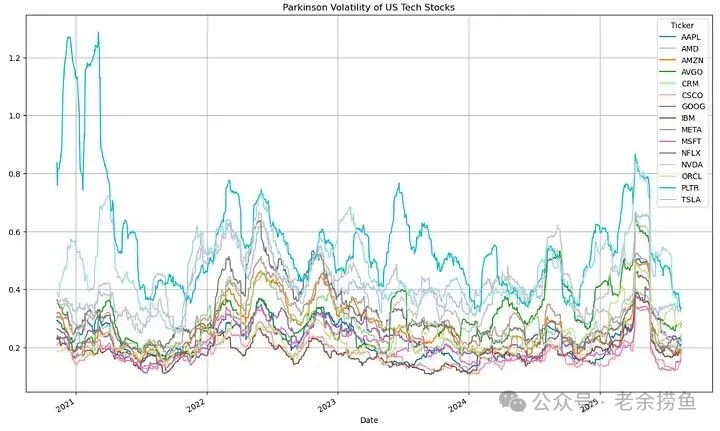
实现代码如下：

def parkinson(price_data, window=30, trading_periods=252, clean=True):

rs = (1.0 / (4.0 * math.log(2.0))) * (
        (price_data["High"] / price_data["Low"]).apply(np.log)
    ) ** 2.0
    def f(v):
        return (trading_periods * v.mean()) ** 0.5
    result = rs.rolling(window=window, center=False).apply(func=f)
    if clean:
        return result.dropna()
    else:
        return result
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
parkinson(data).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Parkinson Volatility of US Tech Stocks')
plt.show()

3.3 Garman-Klass 波动率评估器不仅使用最高价和最低价，还使用开盘价和收盘价。

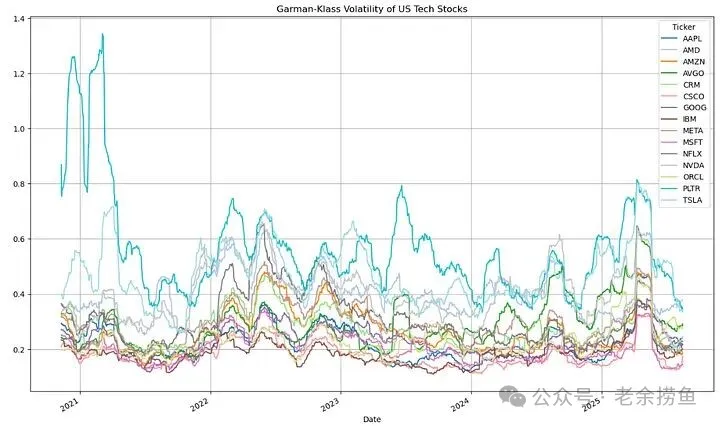
实现代码如下：

def garman_klass(price_data, window=30, trading_periods=252, clean=True):

log_hl = (price_data["High"] / price_data["Low"]).apply(np.log)
    log_co = (price_data["Close"] / price_data["Open"]).apply(np.log)
    rs = 0.5 * log_hl ** 2 - (2 * math.log(2) - 1) * log_co ** 2
    def f(v):
        return (trading_periods * v.mean()) ** 0.5
    result = rs.rolling(window=window, center=False).apply(func=f)
    if clean:
        return result.dropna()
    else:
        return result
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
garman_klass(data).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Garman-Klass Volatility of US Tech Stocks')
plt.show()

3.4 Hodges-Tompkins 波动率是一种调整后的波动率估计量，旨在纠正标准波动率估计量固有的偏差，特别是在处理小样本量时。

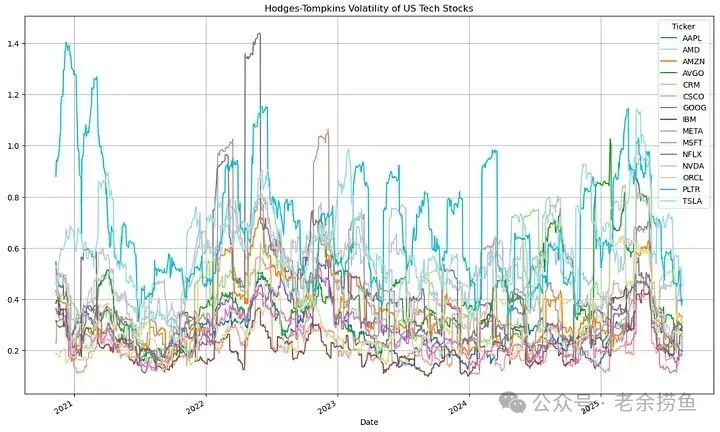
实现代码如下：

def hodges_tompkins(price_data, window=30, trading_periods=252, clean=True):

log_return = (price_data["Close"] / price_data["Close"].shift(1)).apply(np.log)
    vol = log_return.rolling(window=window, center=False).std() * math.sqrt(
        trading_periods
    )
    h = window
    n = (log_return.count() - h) + 1
    adj_factor = 1.0 / (1.0 - (h / n) + ((h ** 2 - 1) / (3 * n ** 2)))
    result = vol * adj_factor
    if clean:
        return result.dropna()
    else:
        return
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
hodges_tompkins(data).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Hodges-Tompkins Volatility of US Tech Stocks')
plt.show()

3.5 Rogers-Satchell 波动率是一种专门针对具有观察到的开盘价、最高价、最低价和收盘价 (OHLC) 的金融时间序列而设计的波动率度量，这使其对于非对数正态分布的资产回报特别有用。

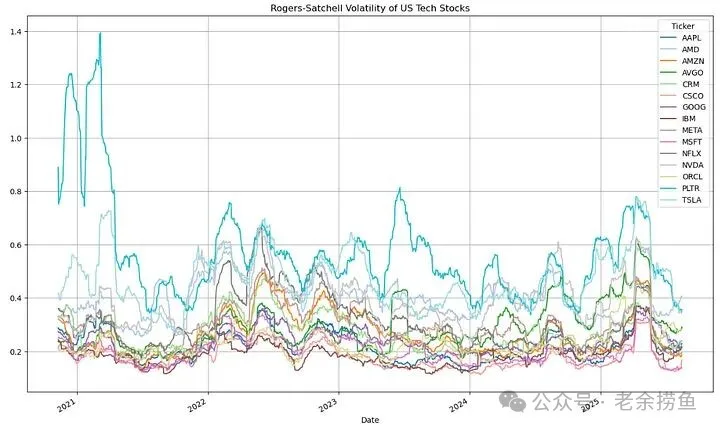
实现代码如下：

def rogers_satchell(price_data, window=30, trading_periods=252, clean=True):

log_ho = (price_data["High"] / price_data["Open"]).apply(np.log)
    log_lo = (price_data["Low"] / price_data["Open"]).apply(np.log)
    log_co = (price_data["Close"] / price_data["Open"]).apply(np.log)
    rs = log_ho * (log_ho - log_co) + log_lo * (log_lo - log_co)
    def f(v):
        return (trading_periods * v.mean()) ** 0.5
    result = rs.rolling(window=window, center=False).apply(func=f)
    if clean:
        return result.dropna()
    else:
        return result
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
rogers_satchell(data).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Rogers-Satchell Volatility of US Tech Stocks')
plt.show()

3.6 杨-张波动率是一种历史波动率的度量，它结合了rogers_satchell和garman_klass的优点。它对于开盘跳涨幅度较大或隔夜跳空高的资产尤其有用。

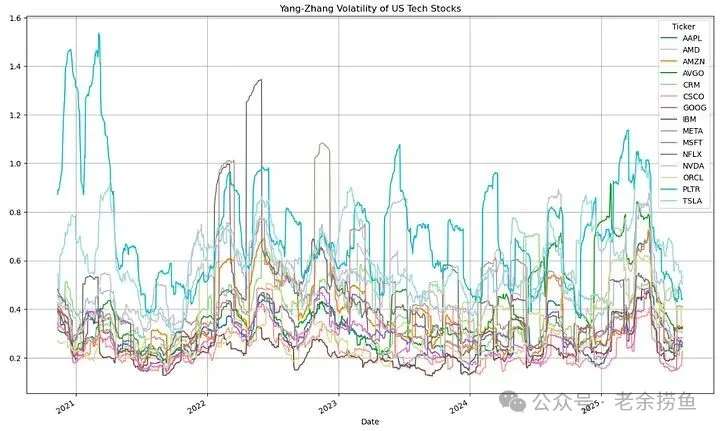
实现代码如下：

def yang_zhang(price_data, window=30, trading_periods=252, clean=True):

log_ho = (price_data["High"] / price_data["Open"]).apply(np.log)
    log_lo = (price_data["Low"] / price_data["Open"]).apply(np.log)
    log_co = (price_data["Close"] / price_data["Open"]).apply(np.log)
    log_oc = (price_data["Open"] / price_data["Close"].shift(1)).apply(np.log)
    log_oc_sq = log_oc ** 2
    log_cc = (price_data["Close"] / price_data["Close"].shift(1)).apply(np.log)
    log_cc_sq = log_cc ** 2
    rs = log_ho * (log_ho - log_co) + log_lo * (log_lo - log_co)
    close_vol = log_cc_sq.rolling(window=window, center=False).sum() * (
        1.0 / (window - 1.0)
    )
    open_vol = log_oc_sq.rolling(window=window, center=False).sum() * (
        1.0 / (window - 1.0)
    )
    window_rs = rs.rolling(window=window, center=False).sum() * (1.0 / (window - 1.0))
    k = 0.34 / (1.34 + (window + 1) / (window - 1))
    result = (open_vol + k * close_vol + (1 - k) * window_rs).apply(
        np.sqrt
    ) * math.sqrt(trading_periods)
    if clean:
        return result.dropna()
    else:
        return result
cmap = plt.get_cmap('tab20') # Colour map (there are many others)
yang_zhang(data).plot(cmap=cmap,figsize=(16, 10))
plt.grid()
plt.title('Yang-Zhang Volatility of US Tech Stocks')
plt.show()

小结如下：

发现大多数科技股的波动率在0.1-0.4之间，但Yang-Zhang波动率显示的范围更广（0.1-0.6），说明考虑到开盘跳空缺口后，波动率更高。

我们可以用Beta系数衡量了股票相对于大盘的波动程度：

• Beta大于1：波动大于大盘（如特斯拉、AMD、Palantir、英伟达）；
• Beta等于1：波动与大盘相当（如微软、谷歌）；
• Beta小于1：波动小于大盘（如IBM、思科）。

第四步： 业绩表现，数字不会说谎

通过量化分析这些公司过去五年的表现，我发现了一些有趣的事情。

4.1 累积收益（CR）明显分成了三个梯队：

• 第一梯队（收益15-31倍）：英伟达、Palantir
• 第二梯队（收益10-15倍）：两只公司
• 第三梯队（收益1-5倍）：其余公司

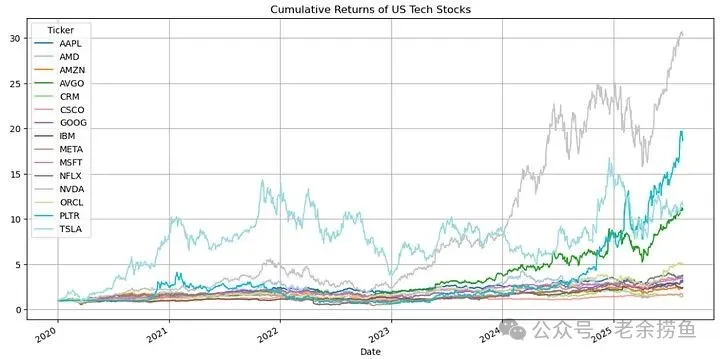
实现代码如下：

%matplotlib inline
import quantstats as qs

# extend pandas functionality with metrics, etc.
qs.extend_pandas()
plt.figure(figsize=(12, 6))
color = iter(cm.tab20(np.linspace(0, 1, len(ticker_list))))
for ticker in ticker_list:
    stock = qs.utils.download_returns(ticker,period="5y")
    c = next(color)
    plt.plot(stock.index, stock, marker='o', linestyle='-', color=c,label=ticker)
    plt.legend()
plt.show()

接着我们使用QuantStats来可视化每日回报

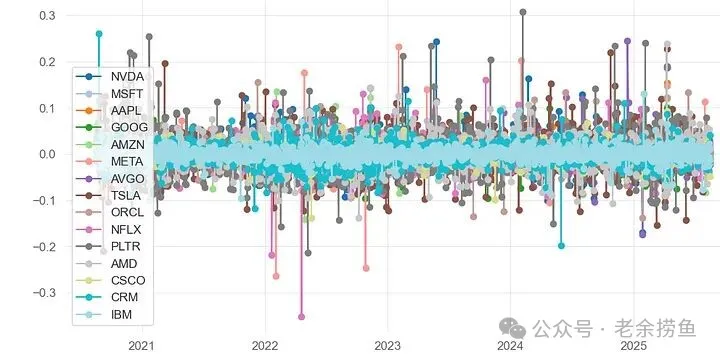
实现代码如下：

%matplotlib inline
import quantstats as qs

# extend pandas functionality with metrics, etc.
qs.extend_pandas()
plt.figure(figsize=(12, 6))
color = iter(cm.tab20(np.linspace(0, 1, len(ticker_list))))
for ticker in ticker_list:
    stock = qs.utils.download_returns(ticker,period="5y")
    c = next(color)
    plt.plot(stock.index, stock, marker='o', linestyle='-', color=c,label=ticker)
    plt.legend()
plt.show()

还可以将每日回报率合并成箱线图

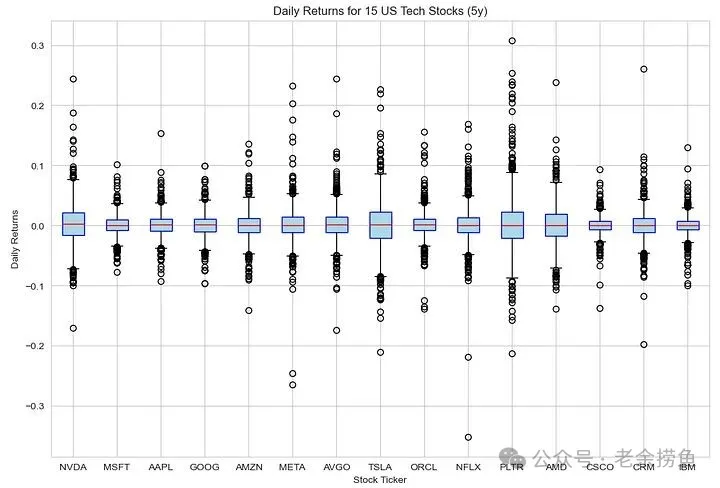
上面的箱线图工具，可以帮您进一步看清股票每日收益况。例如，我们可以轻松地查看回报分布，并确定那些根据当前业绩记录与历史表现来看被高估或低估的资产类别。

实现代码如下：

def boxplot_stock_returns(data, period):
    plt.figure(figsize=(12, 8))
    box_data = [data[ticker].dropna() for ticker in data]  # Drop NA values for plotting
    plt.boxplot(box_data, vert=True, patch_artist=True, boxprops=dict(facecolor='lightblue', color='blue'), medianprops=dict(color='red'))
    plt.xticks(range(1, len(data) + 1), data.keys())
    plt.title(f'Daily Returns for 15 US Tech Stocks ({period})')
    plt.ylabel('Daily Returns')
    plt.xlabel('Stock Ticker')
    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    tickers=ticker_list
    period='5y'
    
    tickers = [ticker.strip() for ticker in tickers]
    stock_data = get_stock_returns(tickers, period)
    
    if all(stock_data[ticker].empty for ticker in tickers):
        print("No data found for the given tickers and period.")
    else:
        boxplot_stock_returns(stock_data, period)

4.2 夏普比率衡量的是风险调整后的收益。微软的夏普比率最高（约0.68），而Palantir和Meta最低（约0.32）。一般来说，夏普比率高于1才算良好，这些科技股似乎都没达到这个标准。

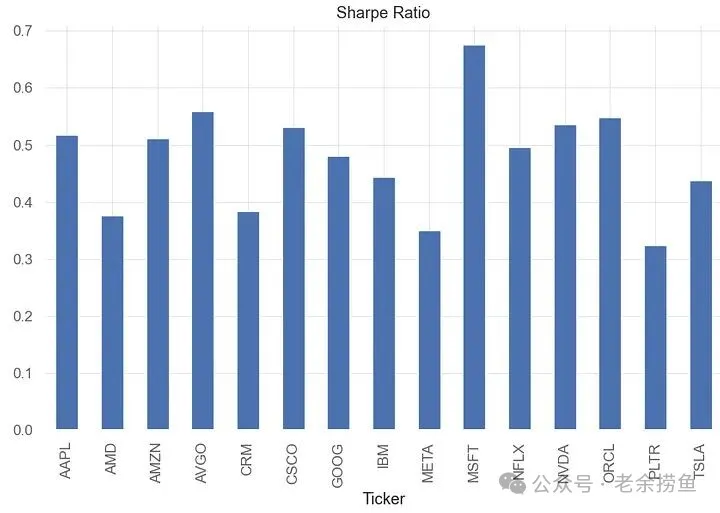
实现代码如下：

import quantstats as qs

# extend pandas functionality with metrics, etc.
qs.extend_pandas()
# fetch the daily returns for a stock
stock = qs.utils.download_returns(ticker_list)
# show sharpe ratio
qs.stats.sharpe(stock)
# or using extend_pandas() :)
stock.sharpe()
Ticker
AAPL    0.518438
AMD     0.376570
AMZN    0.511526
AVGO    0.559362
CRM     0.384257
CSCO    0.532080
GOOG    0.481013
IBM     0.444401
META    0.350088
MSFT    0.675467
NFLX    0.496179
NVDA    0.536758
ORCL    0.548576
PLTR    0.324752
TSLA    0.437640
dtype: float64
stock.sharpe().plot.bar(title='Sharpe Ratio')
plt.show()

4.3 索提诺比率只考虑下行风险，更能反映真正的风险调整收益。微软继续表现的最好（约0.71），Palantir和Meta最差（约0.38）。

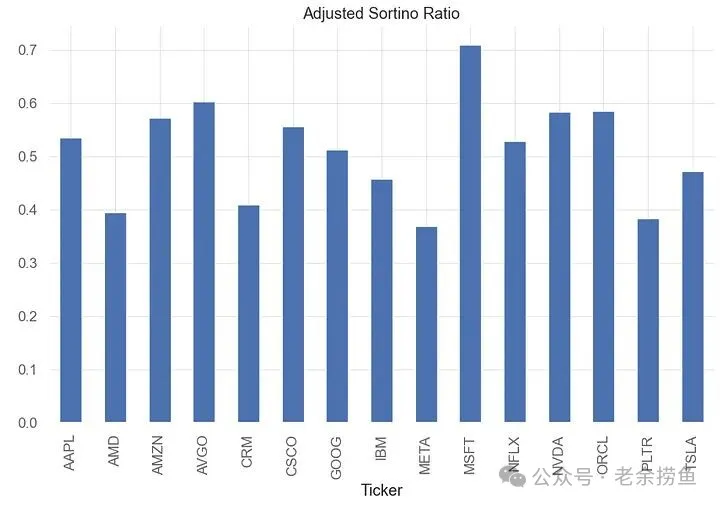
实现代码如下：

stock.adjusted_sortino().plot.bar(title='Adjusted Sortino Ratio')
plt.show()

第五步 最大回撤，你能承受多大亏损？

5.1 最大回撤是非常重要的风险指标，它告诉你可能面临的最大亏损。

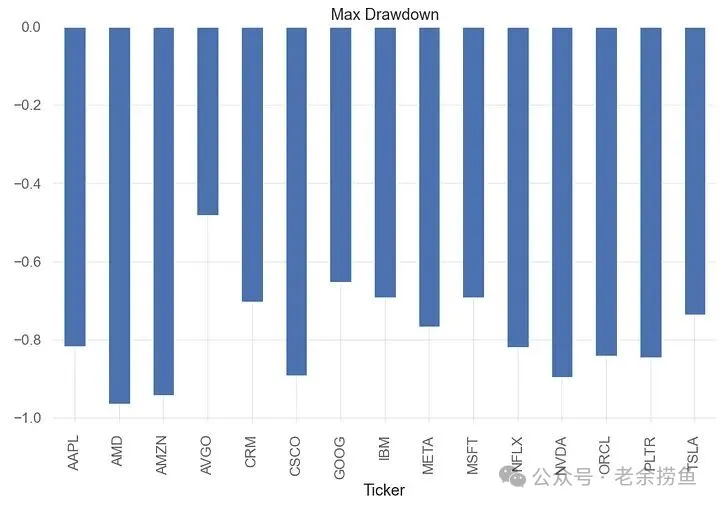
如图：有8家科技公司的历史最大回撤超过80%：苹果、AMD、亚马逊、思科、网飞、英伟达、甲骨文和Palantir。博通的最大回撤最小（约48%），相对较稳健。

这意味着如果你在高点买入，可能需要承受超过80%的亏损才能等到回升。不是每个人都能承受这种压力。

博通的最大回撤最小（约48%），相对较稳健。

代码如下：

md = qs.stats.max_drawdown(stock)

print(md)

Ticker
AAPL   -0.818014
AMD    -0.965895
AMZN   -0.944042
AVGO   -0.483000
CRM    -0.704958
CSCO   -0.892584
GOOG   -0.652948
IBM    -0.693956
META   -0.767361
MSFT   -0.693862
NFLX   -0.819904
NVDA   -0.897224
ORCL   -0.841943
PLTR   -0.846154
TSLA   -0.736322
dtype: float64

stock.max_drawdown().plot.bar(title='Max Drawdown')
plt.show()

5.2 计算下行风险（Ulcer Index）是衡量回撤的深度和持续时间，提供下行风险的综合衡量标准。

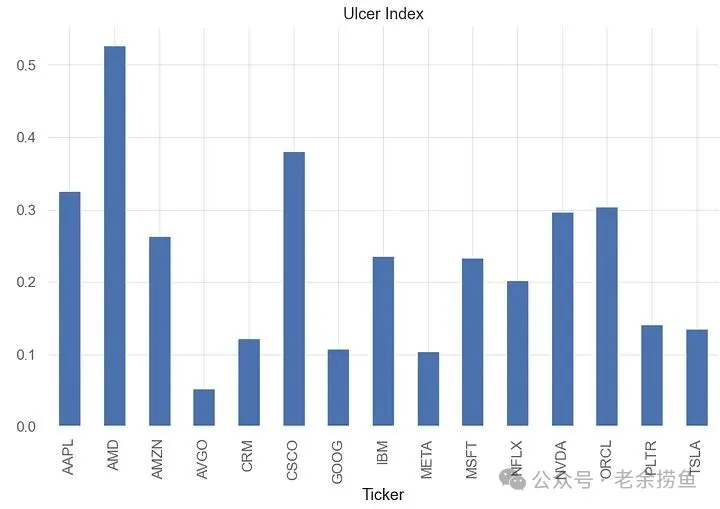
UI 值越大（参见 AMD、CSCO、NVDA、ORCL）意味着较高的下行风险，表明资产在指定的计算周期内从其峰值价格经历了重大、深度和/或长时间的回撤。投资者应将较大的 UI 值解释为下行波动性较大的迹象，这可能不太适合那些风险承受能力较低的人，但对于寻求潜在更高回报的高风险投资者来说可能是可以接受的。

实现代码如下：

stock.ulcer_index().plot.bar(title='Ulcer Index')
plt.show()

5.3 宁静指数（SI）是一种综合风险调整回报指标，它一般和下行风险考虑因素结合在一起使用。

我们可以看到 AVGO 的最大 SI 值为 29.147。

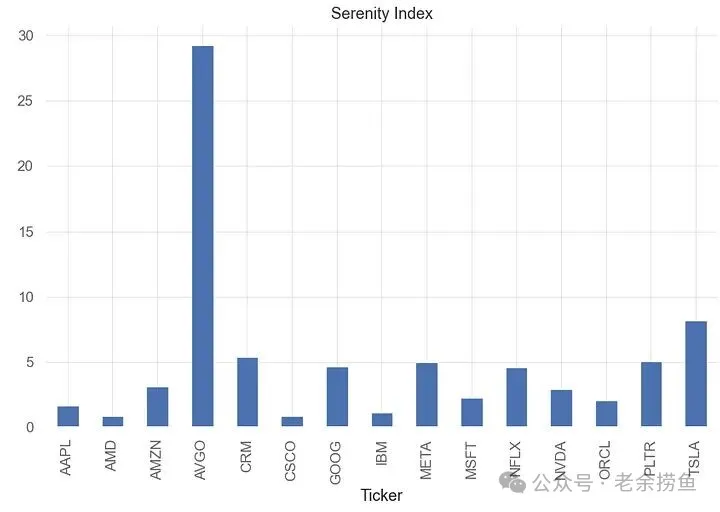
实现代码如下：

si = qs.stats.serenity_index(stock)
print(si)

Ticker
AAPL     1.665390
AMD      0.872389
AMZN     3.153561
AVGO    29.147167
CRM      5.421446
CSCO     0.882820
GOOG     4.707879
IBM      1.122143
META     4.983848
MSFT     2.243300
NFLX     4.628437
NVDA     2.935486
ORCL     2.064152
PLTR     5.007560
TSLA     8.191038
dtype: float64

stock.serenity_index().plot.bar(title='Serenity Index')
plt.show()

中篇总结

今天我们完成了这三项数据分析：

• 风险水平：衡量投资这些公司的风险；
• 业绩表现：回顾历史收益情况；
• 最大回撤：你能承受多大亏损？

在最后一篇中我们将完成等所有内容。

• 公众关注度：了解市场情绪。
• 综合评估：AI投资的价值真相。
• 观点总结：如何科学投资科技股。

请有兴趣的朋友持续关注。

#关键词：
#AI投资 #Python量化 #美股科技股 #投资组合优化 #风险收益分析

---

感谢您阅读到最后，希望这篇文章为您带来了新的启发和实用的知识！如果觉得有帮助，请不吝点赞和分享，您的支持是我持续创作的动力。祝您投资顺利，收益长虹！如果对文中内容有任何疑问，欢迎留言，我会尽快回复！